Asset Management
This section discusses how to manage the assets held in VIRA. I start with a discussion of VIRA’s tail risk hedging strategies which are an integral part of asset management. And then, I briefly discuss how VIRA allocates the capital under control to various classes of assets. This section ends with an illustration of the Monte Carlo simulation analysis results based on a hypothetical asset allocation and implementation of the tail risk hedging strategies. The results show the probability that the Payout Account becomes insolvent with different payout rates over various payout periods, the expected balance of the Reserve Account upon insolvency of the Payout Account, and the expected annuity income if the balance is converted into an SPIA.

Tail Risk Hedging
“Far more money has been lost by investors preparing for corrections, or trying to anticipate corrections, than has been lost in corrections themselves.” – Peter Lynch
There have been 22 market crashes/selloffs since 1817, when the NYSE was created, which means that a market crash/selloff occurs every nine years on average in the US stock market. Therefore, market crashes are indeed a rare tail event. Most prospective VIRA buyers are expected to be in their 50s and 60s with low-risk tolerance. For that cohort of investors, the market crashes they are expected to encounter a few times in the rest of their life could have a lifelong adverse impact on their retirement savings. The reason is that they may not have sufficient investment time to recuperate the capital loss they suffer from a market crash if they maintain a buy-and-hold policy and attempt to ride out the tail event periods. Even the mere possibility of a market crash might have an adverse effect on their unhedged retirement portfolio since the expectation of a severe capital loss might hinder their rational financial decision-making process. Therefore, for those investors in their 50s and 60s with low tail risk tolerance, tail risk hedging of their retirement assets is essential to their post-retirement financial welfare. VIRA offers retail investors tail risk hedging that has been available only to institutional investors.
There are two approaches to tail risk hedging: dynamic asset allocation and direct tail risk hedging. Advocates of dynamic asset allocation argue that it is cost-effective. Their argument is based on the premise that tail risk hedging generates a trading loss because market crashes are rare and carry an opportunity cost caused by the shift of capital from the return-generating assets to an unprofitable tail risk hedge portfolio. Such a premise does not consider an equity premium that the shift toward a more conservative asset composition would cause to forgo. Furthermore, Leibowitz and Bova (2010) and Bhansali (2010) suggest that a tail risk hedge portfolio provides liquidity to allow investors to exploit the opportunities created by market crashes/selloffs.
We have developed direct tail risk hedging strategies, a core part of VIRA, over several years. The strategies require allocating as little as 0.5% of the AUM of the Payout Account to a portfolio dedicated to tail risk hedging. The dedicated tail risk hedge portfolio consists of two sub-portfolios: a permanent, passive hedge portfolio and an actively managed one. The former portfolio is designed to generate an income regularly. At the same time, the latter is constructed to incur a trading loss without market crashes but yield an outsize trading gain in a tail event. The dedicated tail risk hedge portfolio in isolation is designed to make a non-negative return even if a market crash never happens in the future, distinct from most other tail risk hedging strategies.
The following table compares the performance of VIRA with that of S&P 500 TR in the market crash periods of October 2008 through February 2009, January 2020 through March 2020, and January 2022 through December 2022. When S&P 500 TR made a COLA (cost-of-living adjusted) return of -51.70%, -19.95%, and -23.22%, respectively, during those three periods, the Payout Account of VIRA would have returned COLA 28.45%, COLA -2.37%, and COLA -19.63%, respectively, and the Reserve Account COLA 15.32%, COLA 9.90%%, and COLA -23.31%, respectively. The impressive performance of AUM of the Payout and Reserve Accounts in the first two market crash periods verifies the effectiveness of VIRA’s tail risk hedging system. The relatively poor performance of the Payout and Reserve Account in the 2022 market crash period resulted from no corresponding spike of VIX, a major variable of the tail risk hedging system, and a rare lockstep movement between the equity and bond markets.
| Drawdowns in the market crash periods | |||
| Market Crash Period | Inflation-Adjusted Drawdown | ||
| Payout Account Asset Portfolio | Reserve Account Asset Portfolio | S&P 500 TR | |
| 11/2007 – 2/2009 | 28.45% | 15.32% | -51.70% |
| 1/2020 – 3/2020 | -2.37% | 9.90% | -19.95% |
| 1/2022–12/2022 | -19.63% | -23.31% | -23.22% |
Asset Allocation
According to a recent report on retirement assets by the Investment Company Institute (ICI), equities and equity funds account for more than 50% of IRAs and DC plan funds held by individuals in their sixties. In light of prospective VIRA buyers’ revealed risk and return preferences, VIRA takes an equity-tilted approach to managing assets held in the Payout Account. Another reason is that VIRA’s tail risk hedging system protects the AUM of the Payout Account from stock market crashes. In contrast, the AUM in the Reserve Account is invested in fixed-income securities, commodities, and other assets deemed uncorrelated or negatively correlated with equities. The purpose is to protect AUM in the Reserve Account when the Payout Account goes under due to stock market crashes/selloffs.
The expected return is only part of the equation in asset management. Investment risk is an even more critical part in light of the objective of VIRA asset management, which is to meet payout obligations and preserve capital. Furthermore, Bhansali et al. (2014) find that the expected maximum drawdown of a portfolio rests primarily on volatility. To control volatility, therefore, VIRA will diversify AUM across asset classes, countries, industries, and factors. In particular, equity investment will be extended to the greater China region and Japanese markets that have historically a low correlation with the US market. Furthermore, VIRA will construct the asset portfolio in the Payout Account to resemble the minimum variance portfolio.
Monte Carlo Simulation Analysis

In this section, we conduct a Monte Carlo simulation analysis based on the historical risk and return of several benchmark indexes to estimate the probability of depletion of the balance in the Payout Account and the expected balance in the Reserve Account upon insolvency of the Payout Account.
We consider a newly retired 65-year-old man with a five-year-younger spouse who has joint retirement savings of $100. Suppose that the couple deposits their retirement savings with VIRA, which are split $90/$10 between the Payout Account and the Reserve Account. VIRA would transfer one-twelfth of COLA $2 from the Payout Account to the Reserve Account every month. The couple is assumed to select one of four different payout rates of 3, 4, 5, and 6% of the COLA value of the money deposited with the Payout Account ($90). VIRA is assumed to charge an annual management fee of 35 and 20 bps on the Payout and Reserve Account balance, respectively.
The following table shows the risk and return statistics of various benchmark indexes that constitute the Payout and Reserve Account asset portfolios used for the Monte Carlo simulation analysis. The Payout Account asset portfolio consists of S&P 500, Nasdaq 100, small caps, high-dividend yield stocks with a weight of 17.5% each, gold and long-term Treasury bonds with a weight of 12.5% each, and short-term Treasury bills and a tail risk hedge portfolio with a weight of 4.5% and 0.5%, respectively.
Based on the historical risk and return of component assets, the Payout Account asset portfolio has a monthly mean logarithmic real return of 0.88% and a monthly standard deviation of 4.41%. The Reserve Account comprises gold, long-term Treasury bonds, and intermediate-term Treasury bonds, each with a 30% weight, and short-term Treasury bills with a 10% weight. As a result, the Reserve Account asset portfolio has a monthly logarithmic real mean return of 0.22% and a monthly standard deviation of 2.28%.
One may notice that the expected monthly logarithmic real return for the Payout Account used in the Monte Carlo simulation analysis is significantly higher than the historical mean return for a traditional 60/40 portfolio. VIRA’s tail risk hedge portfolio is the major contributor to enhancing the expected real return. The expected monthly real return without the tail risk hedge portfolio would be 0.51% compared with 0.88% with the hedge portfolio. Although we cannot guarantee the future performance of the tail risk hedge portfolio, we are cautiously confident in VIRA’s tail risk hedging strategies.
Following Feldstein and Ranguelova (2000), the simulation is based on the premise that the future mean return is itself uncertain, and there is a monthly variant in the actual returns, given an estimated mean return. I proceed with the simulation by drawing a future mean return from a normal distribution of the mean logarithmic real return and standard error for the Payout and Reserve Account asset portfolios. I then randomly generate 144, 180, 240, 300, 360, and 420 monthly returns from a distribution with that mean return and sample standard deviation. I use these estimated returns to simulate the probability of depletion of the balance in the Payout Account and the expected balance of the Reserve Account after 12, 15, 20, 25, 30, and 35 years of investment and payouts. I repeat this process 10,000 times and tabulate the resulting ruin probability of the Payout Account by the payout rate and distribution of the balance of the Reserve Account.
The following figure exhibits the ruin probability of the Payout Account after 12 to 35 years of investment with the four different payout rates. The graphical representation reveals that the Payout Account with a 3% or 4% payout rate is most likely to remain solvent with a ruin probability of below 8% after 35 years of payouts. In contrast, the Payout Account with a 6% payout rate alone has a ruin probability of as high as 26% in 35 years, separate from the rest of the payout rates. This simulation result suggests that a 6% payout rate or higher is not a viable choice for the couple.
The ruin probability with a 5% payout rate remains below 3% after 15 years and jumps to above 7% in 20 years. Then, it leaps further to 11%, 14%, and 16% in 25, 30, and 35 years, respectively. This finding suggests that the Payout Account with a 5% payout rate has a reasonably good chance of remaining solvent in 20 years. Even if the balance is depleted in the Payout Account in 20 years, Table 4 indicates that the Reserve Account would have accumulated a median COLA balance of $68 by then. Table 5 shows how much NoneCOLA annual income the couple would have if they converted the balance in the Reserve Account into an SPIA for a joint life couple in various years after the initial investment. According to the table, the couple would have a median NoneCOLA annual income of $6.8 for the rest of their lives at the ages of 85 and 80. This means they would likely secure a lifetime annual NoneCOLA payout rate of as high as 6.8%.
The simulation results show the advantage of VIRA compared to traditional life annuities. Table 5 shows that the median COLA balance of the Reserve Account could grow to $88 in 25 years, $110 in 30 years, and $135 in 35 years, thanks to the power of compounding. This simulation result suggests that the couple might accumulate enough balance in the Reserve Account to cover LTC or critical illness expenses or pass it to their beneficiaries.
| Payout Account asset portfolio composition | ||||
| Asset | Weight | Monthly Mean Logarithmic Real Return | Standard Deviation | Estimation Period |
| S&P 500 | 17.5% | 0.56% | 5.39% | 1/1926 to 12/2022 (S&P 90 prior to 3/1957) |
| Nasdaq 100 | 17.5% | 0.78% | 6.98% | 12/1985 to 12/2022 |
| High-Dividend Yield Stocks | 17.5% | 0.67% | 5.51% | 1/1927 to 12/2022 |
| Small-Cap Stocks | 17.5% | 0.66% | 5.52% | 12/1956 to 12/2022 |
| Gold | 12.5% | 0.30% | 5.50% | 1/1970 to 12/202 |
| Long-Term Treasury Bonds | 12.5% | 0.18% | 2.61% | 1/1926 to 12/2022 |
| Short-Term Treasury Bills | 4.5% | 0.02% | 0.53% | 1/1926 to 12/2022 |
| Tail Risk Hedge Portfolio | 0.5% | 0.40% | 4.78% | 1/2007 to 12/2022 |
| Payout Account | 100% | 0.88% | 4.41% | Mean return over the period corresponding to each asset class: SD over 1/2007 to 12/2022 |
| Reserve Account asset portfolio composition | ||||
| Asset | Weight | Monthly Mean Logarithmic Real Return | Standard Deviation | Estimation Period |
| Gold | 30% | 0.30% | 5.50% | 1/1970 to 12/2022 |
| Long-Term Treasury Bonds | 30% | 0.18% | 2.61% | 1/1926 to 12/2022 |
| Intermediate-Term Treasury Bonds | 30% | 0.13% | 1.47% | 1/1926 to 12/2022 |
| Short-Term Treasury Bills | 10% | 0.02% | 0.53% | 1/1926 to 12/2022 |
| Reserve Account | 100% | 0.22% | 2.28% | Mean return over the period corresponding to each asset class: SD over 1/1970 to 12/2022 |

Following Feldstein and Ranguelova (2000), the simulation is based on the premise that the future mean return is itself uncertain, and there is a monthly variant in the actual returns, given an estimated mean return. We proceed with the simulation by drawing a future mean return from a normal distribution of the mean logarithmic real return and standard error for the Payout and Reserve Account asset portfolios. We then randomly generate 144, 180, 240, 300, 360, and 420 monthly returns from a distribution with that mean return and sample standard deviation. We use these estimated returns to simulate the probability of depletion of the balance in the Payout Account and the expected balance of the Reserve Account after 12, 15, 20, 25, 30, and 35 years of investment and payouts. We repeat this process 10,000 times and tabulate the resulting ruin probability of the Payout Account by the payout rate, and distribution of the balance of the Reserve Account.
The figure below exhibits the ruin probability of the Payout Account after 12 to 35 years of investment with the four different payout rates. The graphical representation reveals that the Payout Account with a payout rate of 3% or 4% is most likely to remain solvent with a ruin probability of below 3% after 35 years of investment and payouts. In contrast, the Payout Account with a 6% payout rate stands alone with a ruin probability of as high as 14% in 35 years, separate from the rest of the payout rates. This simulation result suggests that a payout rate of 6% or higher is not a viable choice for the couple.
The ruin probability with a 5% payout rate remains below 1% after 15 years and jumps to around 3% in 20 years. Then, it leaps further to 5%, 6%, and 7% in 25, 30, and 35 years, respectively. This suggests that the Payout Account with a 5% payout rate has a fairly good chance of remaining solvent in 20 years. Even if the balance is depleted in the Payout Account in 20 years, the first table below indicates that the Reserve Account would accumulate a median COLA balance of $72 by that time. The second table below shows how much NoneCOLA annual income the couple would have if they chose to convert the balance in the Reserve Account into an SPIA for a joint life couple in various years after the initial investment. According to the table, the couple would have a NoneCOLA annual income of $7 for the rest of their lives at the ages of 85 and 80. This means that they would be able to secure a lifetime annual NoneCOLA payout rate of as high as 7%.
The simulation results make evident the advantage of VIRA compared to traditional life annuities. The second table below shows that the median COLA balance of the Reserve Account could grow to $94 in 25 years, $119 in 30 years, and $148 in 35 years, thanks to the power of compounding. This simulation result suggests that the couple might be able to accumulate enough balance in the Reserve Account to cover LTC or critical illness expenses and/or pass it to their beneficiaries.
| Estimated probability of depletion of the balance in the Payout Account by the payout rate |
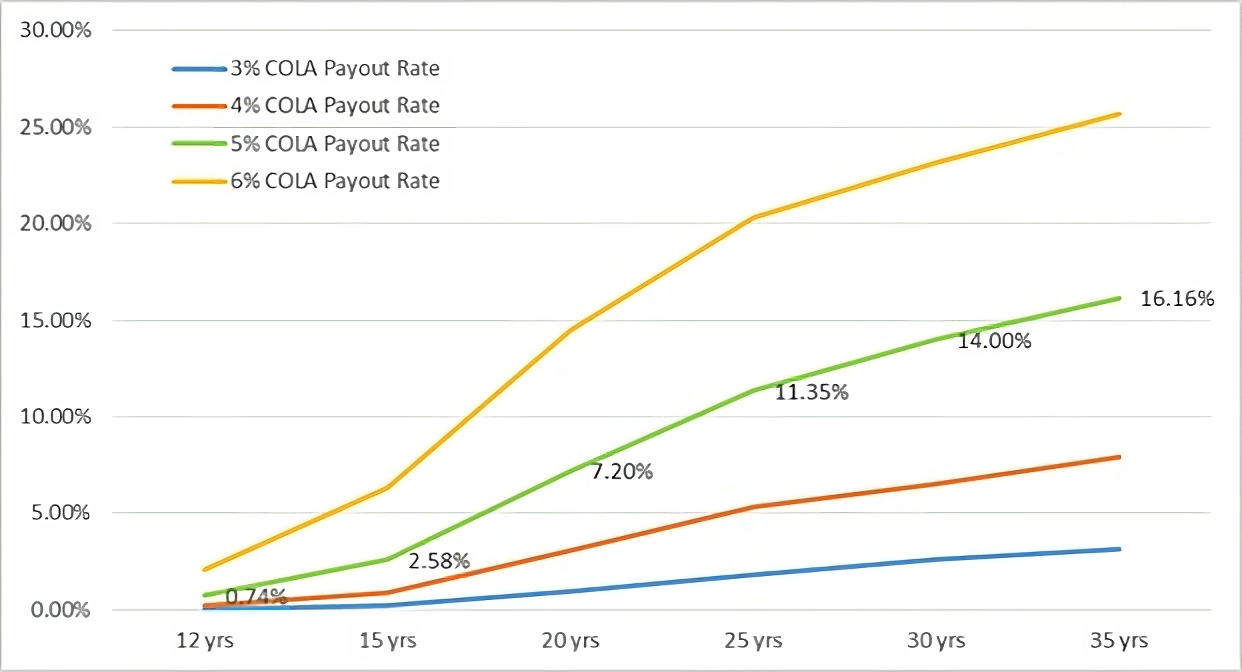 |
*COLA is short for Cost-Of-Living-Adjusted
| Summary statistics of the simulated distribution of the balance of the Reserve Account over 12 to 35 years | |||||||
| Years since investment | Mean | SD | Min | Q1 | Median | Q3 | Max |
| 12 yrs. | $42.28 | $8.18 | $21.08 | $36.46 | $41.39 | $47.05 | $91.58 |
| 15 yrs. | 52.30 | 11.24 | 23.84 | 44.23 | 50.99 | 58.72 | 116.74 |
| 20 yrs. | 70.74 | 17.52 | 29.88 | 58.22 | 68.33 | 80.78 | 159.93 |
| 25 yrs. | 91.81 | 25.41 | 32.00 | 73.45 | 88.04 | 105.87 | 259.79 |
| 30 yrs. | 116.04 | 35.68 | 38.71 | 90.31 | 110.27 | 135.30 | 383.39 |
| 35 yrs. | 143.50 | 47.73 | 38.67 | 109.89 | 135.10 | 168.52 | 484.43 |
| Conversion of the balance in the Reserve Account into an SPIA for a joint life couple | ||||||
| 12 yrs. | 15 yrs. | 20 yrs. | ||||
| COLA Balance | NoneCOLA Annual Annuity Income | COLA Balance | NoneCOLA Annual Annuity Income | COLA Balance | NoneCOLA Annual Annuity Income | |
| Minimum | $21 | $1.61 | $24 | $1.84 | $30 | $2.99 |
| Median | $41 | $3.15 | $51 | $3.91 | $68 | $6.77 |
| Maximum | $92 | $7.06 | $117 | $8.98 | $160 | $15.93 |
| 25 yrs. | 30 yrs. | 35 yrs. | ||||
| COLA Balance | NoneCOLA Annual Annuity Income | COLA Balance | NoneCOLA Annual Annuity Income | COLA Balance | NoneCOLA Annual Annuity Income | |
| Minimum | $32 | $4.22 | $39 | n/a | $39 | n/a |
| Median | $88 | $11.60 | $110 | n/a | $135 | n/a |
| Maximum | $260 | $34.26 | $384 | n/a | $484 | n/a |
 Login
Login
